Time decay is often described as the options seller's best friend and the buyer's worst enemy. Understanding how Theta works and its impact on popular strategies like Iron Condors, Iron Butterflies, and Strangles can significantly improve your trading performance.

1️⃣ Understanding Theta: The Silent Profit Engine

Theta measures the rate at which an option's value decays over time, assuming all other variables remain constant. In dollar terms, it represents how much value an option loses daily due to time decay.

Key Theta Characteristics:

• Highest for At-The-Money (ATM) options
• Accelerates exponentially in the last weeks before expiration
• Always negative for long options and positive for short options
• Non-linear behaviour that intensifies closer to expiration

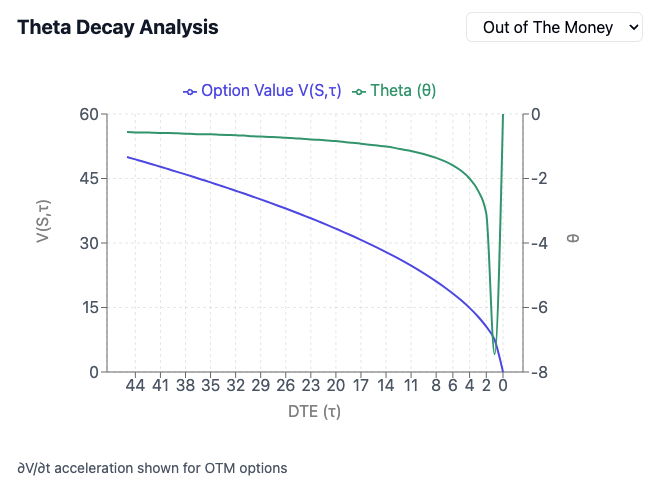
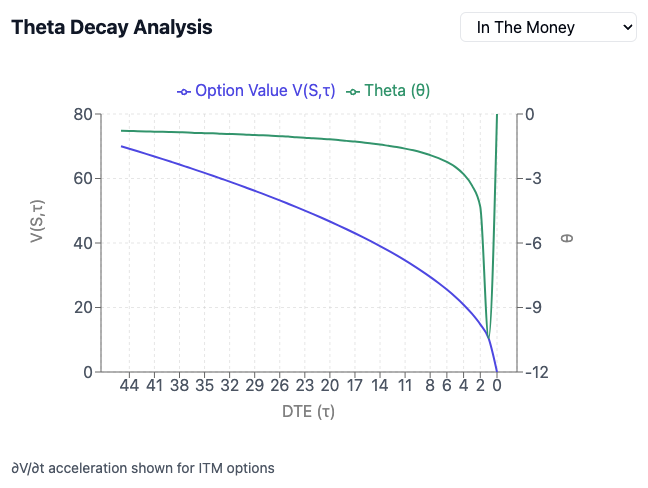
The behaviour of theta decay is defined by several fundamental characteristics that shape how options lose value over time. Theta reaches its peak intensity in At-The-Money (ATM) options because these contracts carry the highest amount of extrinsic value, acting like an hourglass with the most sand to lose. As you move away from the strike price in either direction (ITM or OTM), theta's impact diminishes, similar to how a melting ice cube shrinks faster in its centre. The decay pattern follows a non-linear trajectory that intensifies dramatically in the final weeks before expiration - much like a snowball rolling downhill, gathering speed as it descends. This acceleration is particularly pronounced in the last 21 days, where options might lose value two to three times faster than during earlier periods. The relationship between position direction and theta is immutable: long options always face negative theta (working against you), while short options benefit from positive theta (working for you), making time for either your enemy or ally depending on your position. For instance, an ATM call option 45 days from expiration might lose $0.50 per day, but the same option at 10 days from expiration could lose $2.00 daily, demonstrating the exponential nature of this decay. This non-linear behaviour creates both opportunities and risks, requiring traders to constantly balance the accelerating decay against increasing gamma exposure as expiration approaches.

2️⃣ Theta Calculation in Options Theory

The theta (Θ) measures an option's time decay and is calculated as the partial derivative of the Black-Scholes formula with respect to time. The formula differs for calls and puts:

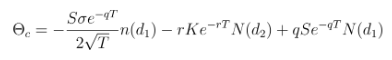
For calls

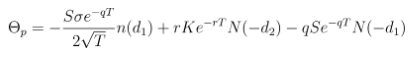
For puts

Where:

• S: Underlying price
• K: Strike price
• r: Risk-free rate
• T: Time to expiration
• σ: Implied volatility
• q: Dividend yield
• n(x): Standard normal PDF
• N(x): Standard normal CDF

The Rust implementation of theta calculation closely follows the Black-Scholes derivatives formula using idiomatic Rust features. The theta function accepts an Options struct containing market parameters and uses pattern matching to handle calls and puts separately. The calculation first computes auxiliary values d1 and d2 using safe numeric types (

PositiveF64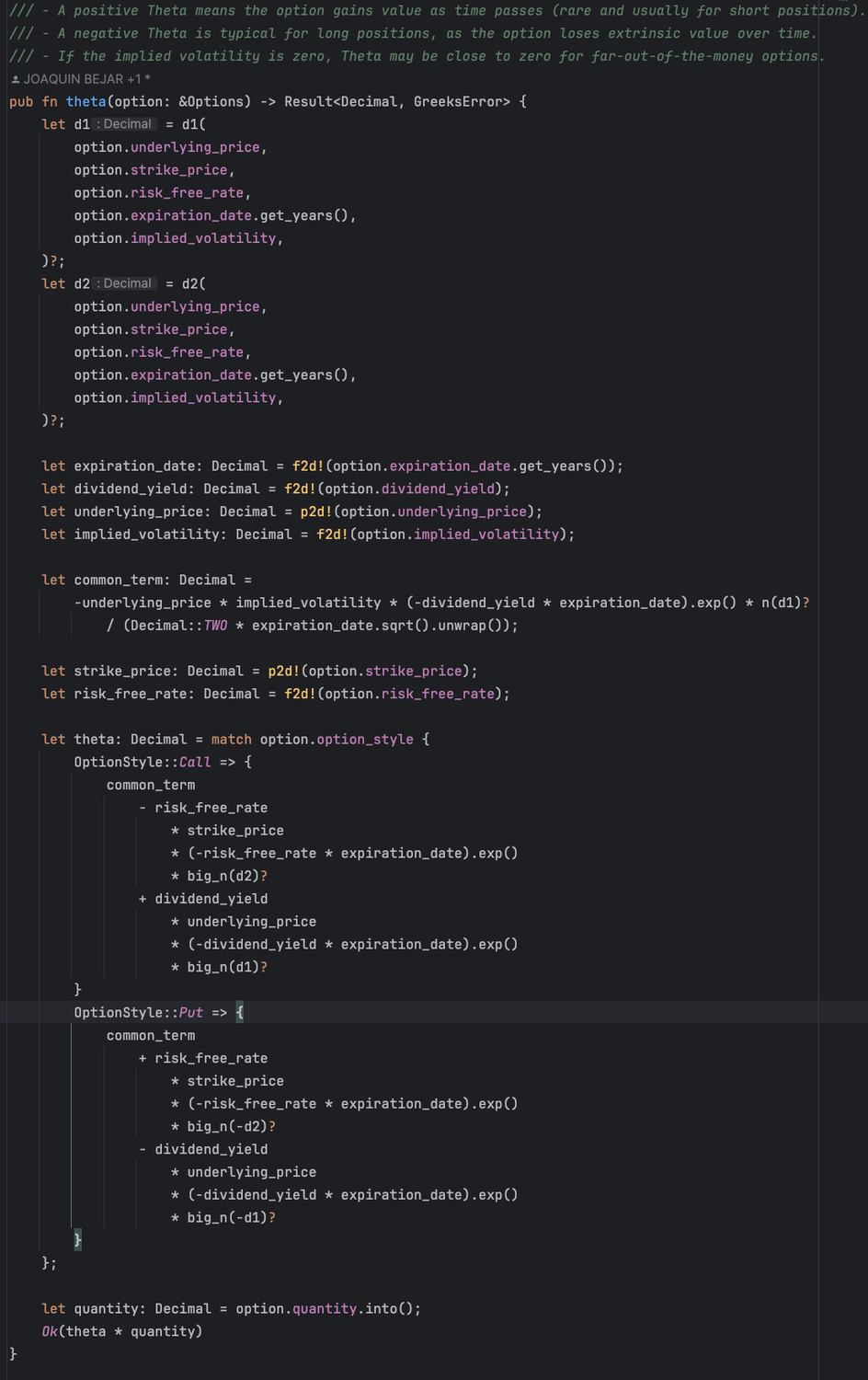

https://github.com/joaquinbejar/OptionStratLib/blob/main/src/greeks/equations.rs#L195

The Delta-Theta Relationship

A critical aspect that many traders overlook is how Theta can offset Delta gains. Consider this scenario: you buy a call option with a correct directional prediction (positive Delta), but the underlying moves too slowly. The daily Theta decay might exceed your Delta gains, resulting in a net loss despite being directionally right.

3️⃣ Optimizing Theta Decay

The art of optimizing Theta decay centres on three critical dimensions: timing, volatility conditions, and strike selection. The most effective Theta decay typically occurs between 45 and 21 days until expiration, often called the "sweet spot" where options lose value at an accelerating rate while still providing adequate time for position management. For optimal results, traders should prioritize selling options when implied volatility is elevated (typically when IV rank > 50%), as this increases premium collection and provides a cushion against adverse market movements. Strike selection plays a crucial role - At-the-money options experience the highest absolute Theta decay but carry the highest gamma risk; therefore, selling slightly OTM options often provides a better risk-adjusted return. Additionally, consideration must be given to the volatility skew and upcoming market events that could impact decay patterns. The key to successful Theta optimization lies in balancing these factors while maintaining strict position sizing - typically limiting any single position to 1-5% of portfolio value to manage the risk of gamma acceleration in the final weeks before expiration.

Considerations Charm Effect

Charm, also known as Delta decay, plays a crucial role in options position management by measuring how Delta changes as time passes. This second-order Greek becomes particularly significant in the last month before expiration, where its effects can dramatically impact delta-neutral positions. For example, an ATM option with 0.50 delta might see its delta drift to 0.55 or 0.45 purely due to time passage, even if the underlying price remains unchanged. This effect is most pronounced in options near the strike price and can be especially challenging during holiday periods or long weekends, where multiple days of Charm effect hit the position simultaneously. Smart traders factor in Charm when planning position adjustments, particularly for iron condors and other multi-leg strategies where delta neutrality is key. One practical approach is to slightly skew initial positions against the expected Charm effect, essentially "pre-adjusting" for the anticipated delta drift. Additionally, positions with significant negative gamma, such as short strangles, require extra attention to Charm as their delta exposure can change rapidly, especially during the final weeks before expiration.

4️⃣ The Theta Battle: Longs vs. Shorts

Options are decaying assets by nature, making time the constant ally of option sellers and the perpetual enemy of option buyers. When you buy an option, you purchase a right with intrinsic value (if In-the-money) and time value. Still, this time value continuously erodes every day until expiration - like an ice cube melting in your hand. Option sellers exploit this inevitable decay by essentially becoming "insurance providers," collecting premiums upfront and benefiting from the natural erosion of time value. Think of it as renting out an asset that depreciates - the renter (option buyer) pays for the full value upfront, but with each passing day, they hold an asset worth less than the day before. This decay accelerates as expiration approaches, similar to how a car's value drops more rapidly in its early years. Short option positions profit from this decay (positive theta), while long positions suffer (negative theta), making time a critical factor in options trading. This fundamental characteristic explains why many professional options traders prefer to be net sellers of options, structuring their strategies to harness this natural time decay while carefully managing the associated risks.

5️⃣ The Volatility-Theta Relationship

The relationship between implied volatility and theta decay presents one of the most fascinating dynamics in options trading. Higher implied volatility results in more significant option premiums, leading to more substantial theta decay - think of it as a steeper hill to slide down. This relationship creates an amplified effect where high-IV environments offer more attractive premium-selling opportunities and carry more significant risks. For instance, an ATM option with 30 DTE might have a theta of -0.05 when IV is at 15%, but the same option could have a theta of -0.15 when IV sits at 45%. This non-linear relationship explains why professional traders often become more aggressive option sellers during high volatility periods, notably when IV ranks above its 75th percentile. However, this higher theta decay comes with a crucial caveat: the increased premium reflects the market's expectation of more significant price movements, making position sizing and risk management even more critical. Smart traders don't just chase high IV for the larger theta decay; they carefully weigh this enhanced decay against the increased probability of significant adverse moves, often reducing position sizes as volatility expands while maintaining their overall theta budget.

6️⃣ Weekend Effect on Theta

The weekend effect in options trading offers a unique dynamic where theta decay continues its relentless march even when markets are closed. While options are priced using calendar days rather than trading days, the market must account for three days of time decay (Friday to Monday) in a single trading session. This compression creates interesting opportunities, particularly for option sellers who effectively collect three days' worth of theta in a single day. Think of it as a "theta dividend" paid out on Fridays. Sophisticated traders often exploit this effect by entering short premium positions on Friday afternoons, especially in the last few hours of trading, and closing them on Monday mornings. The effect becomes particularly pronounced on holiday weekends, where four or even five days of decay must be priced into a single session. However, this opportunity comes with its risks - weekend gaps and Monday morning volatility can quickly overwhelm the collected theta, especially during earnings season or in times of market uncertainty. This creates a delicate balance where traders must weigh the enhanced theta collection against the risk of adverse weekend moves, often leading to reduced position sizes but more frequent deployment of this strategy.

Theta Decay During Market Hours vs. Overnight

The distribution of theta decay between market hours and overnight periods reveals a fascinating inefficiency in options markets that savvy traders can exploit. While theta technically decays continuously in calendar time, empirical evidence suggests that options lose more value during market hours than overnight periods. This phenomenon contradicts the theoretical continuous decay model. For instance, a position with a theoretical daily theta of -$30 might lose $20-25 during the 6.5-hour trading session but only $5-10 during the longer overnight period. This asymmetry creates opportunities, particularly during the last two hours of trading when market makers adjust their positions for overnight risk. The effect becomes even more pronounced on Fridays, where the market must price in weekend decay during a single session. Professional traders often structure their entries and exits to capitalize on this intraday decay pattern, preferring to sell premium near the market open when options are relatively expensive and buy back or close positions in the final hours when the day's decay has largely been realized. However, this strategy requires careful consideration of overnight gap risk, especially during earnings seasons or periods of elevated market uncertainty, where the premium for overnight protection can cause options prices to rise into the close.

7️⃣ The Gamma-Theta Trade-off

The relationship between Gamma and Theta represents one of the fundamental trade-offs in options trading, operating like two sides of the same coin. When you sell options to capture Theta, you inherently expose yourself to Gamma risk - an unavoidable mathematical relationship that becomes more pronounced as expiration approaches. Think of Theta as the premium you collect for taking on Gamma risk. This relationship intensifies particularly in the last 21 days before expiration, where the rate of Theta decay accelerates dramatically, and so does your Gamma exposure - like a pendulum swinging faster as it reaches its centre point. For instance, a short ATM option position might generate $50 daily in Theta decay, but a 1% move in the underlying could generate $150 in Gamma losses, creating an asymmetric risk profile. This is why experienced option sellers often close or roll their positions before entering this high-risk period, typically around 21-25 DTE, even if it leaves some potential Theta decay on the table. Understanding this trade-off is crucial: while higher Theta decay might seem attractive, it comes with proportionally higher Gamma risk that can quickly overwhelm any accumulated premium, particularly during swift market moves. The art lies in finding the sweet spot where the Theta decay compensates adequately for the Gamma risk without creating an unsustainable position.

8️⃣ Calendar Spreads: The Theta Differential

Calendar spreads harness the non-linear nature of time decay by exploiting the different decay rates between near-term and longer-dated options. This strategy works because options with different expirations decay at different velocities, like two hourglasses with sand falling at different rates. You're essentially arbitraging the time decay differential when you sell a near-term option and buy a longer-dated one at the same strike. The near-term option decays more rapidly (higher negative Theta), while the longer-dated option protects with its slower decay rate. For example, a 30-day ATM option might have a Theta of -0.05, while a 60-day option at the same strike might only have a Theta of -0.03, creating a positive Theta differential of 0.02 in your favour. This differential typically peaks when the front-month option enters its steepest decay phase (around 21-30 DTE), while the back-month option remains relatively stable. However, this strategy requires careful consideration of implied volatility term structure - if back-month volatility drops more than the front-month, it can offset your Theta gains. The key to successful calendar spreads lies in selecting the optimal combination of expiration dates and managing the position's exposure to volatility skew changes, which can dramatically impact the spread's profitability beyond simple time decay.

9️⃣ Earnings and Theta

Earnings announcements create a unique disruption in the normal pattern of theta decay, transforming it from a smooth, predictable erosion into a binary event with cliff-like characteristics. During the lead-up to earnings, options carry an additional "uncertainty premium" that doesn't decay in the usual manner - instead of the gradual theta decay we typically expect, a significant portion of the option's value is tied to the earnings event itself. This creates what traders call the "volatility crush" effect, where a substantial premium evaporates almost instantly after the announcement, regardless of how many calendar days remain until expiration. For example, an option trading at $3.00 with 30% of its value attributed to earnings uncertainty might suddenly drop to $2.10 immediately following the announcement, essentially experiencing weeks' worth of theta decay in a single moment. This dynamic makes traditional theta-focused strategies particularly risky during earnings seasons, as the elevated premiums that make selling options attractive come with the substantial risk of gap moves that can easily overwhelm any collected premium. Smart traders often either avoid holding short premium positions through earnings entirely or significantly reduce position sizes to account for this binary risk profile, understanding that the normal rules of theta decay temporarily cease to apply during these high-impact corporate events.

🔟 Managing Theta Risk in Long Options

Being long options is like fighting against a constant headwind of time decay, but there are strategic approaches to minimize this persistent drag on your position. The key lies in understanding that not all long-option positions suffer from theta decay equally. Deep ITM options, for instance, carry minimal time value and thus experience less theta decay, making them more efficient for directional plays despite their higher capital requirement. To combat theta burn in long positions, successful traders employ several techniques: using longer-dated options (LEAPS) to benefit from a slower decay rate, although this means paying more upfront premium; implementing diagonal spreads where short, nearer-term options help offset the theta decay of longer-dated longs; or utilizing call/put spreads to reduce the net theta exposure at the cost of capping potential gains. For example, rather than buying a 30-day ATM call for $3.00 with a theta of -0.03 (losing $3 per day), you might buy a 90-day option for $4.50 with a theta of -0.02, sacrificing capital efficiency for a more manageable daily decay. Position timing also becomes crucial - entering long options when IV is relatively low reduces the absolute dollar amount of daily theta decay and provides potential volatility expansion benefits. The art of managing long option positions ultimately balances the threat of time decay against the opportunity for directional or volatility gains while staying within your risk parameters.

1️⃣1️⃣ The "Sweet Spot" for Credit Spreads

Credit spreads exhibit a unique optimal entry and management window that experienced traders call the "sweet spot" - typically between 45 and 21 days until expiration. This timing leverage sits at the intersection of premium collection and risk management, offering the most favourable balance of theta decay against gamma risk. The 45-day entry point is strategic: implied volatility tends to decay more steadily during this period while still providing enough premium to make the trade worthwhile. As we approach 21 days, theta decay accelerates significantly, but so does gamma risk - like walking on increasingly thin ice for higher rewards. For example, a credit spread might collect 30% of its maximum profit in the first 15 days from 45 DTE and another 40% in the next 15 days. Still, the remaining 30% comes with disproportionately higher risk as gamma exposure spikes. Professional traders often target taking profits at 50-75% of maximum potential gain, typically around the 25-30 DTE mark, rather than holding through the higher-risk acceleration period. Position management becomes crucial - what starts as a $1 wide spread collecting $0.35 in premium might be best closed at $0.15, sacrificing potential additional gains to avoid the exponential increase in gamma risk that comes with pursuing those final nickels and dimes.

1️⃣2️⃣ Some conclusions

Success in options trading requires mastering the dual nature of theta decay - its predictable mathematical properties and its nuanced market behaviour. The non-linear acceleration of time decay creates both opportunities and risks that demand careful management.

Key success factors in theta-based trading include:

• Strategic Timing

  • Entry during optimal decay windows
  • Understanding market hours vs overnight decay patterns
  • Leveraging weekend effects for enhanced returns

• Risk Integration

  • Balancing theta capture against gamma exposure
  • Adjusting position sizes based on implied volatility levels
  • Managing correlation risk in multi-leg strategies

• Market Adaptation

  • Modifying strategies during earnings seasons
  • Adjusting for changing volatility environments
  • Rolling positions to maintain optimal decay exposure

• Position Management

  • Setting appropriate profit targets (typically 50-75% of maximum)
  • Implementing mechanical adjustment rules
  • Maintaining portfolio-level theta exposure limits

The path to consistent profitability lies in understanding these principles and developing a systematic approach that adapts to changing market conditions while maintaining strict risk parameters. Successful theta traders combine technical understanding with disciplined execution, treating each position as part of a broader portfolio strategy rather than isolated opportunities.

Remember: Time decay is inevitable, but capturing value requires patience and precision. The most successful traders are those who respect theta's power while remaining vigilant to its associated risks.

Note: This article is for educational purposes only. Options trading involves significant risk. Consult with a qualified financial advisor before implementing any investment strategy.